微分流形(differentiable manifold)，也称为光滑流形(smooh2 manifold)，是拓扑学和几何学中一类重要的空间，是带有微分结构的拓扑流形。 微分流形是微分几何与微分拓扑的主要研究对象，是三维欧式空间中曲线和曲面概念的推广，可以有更高的维数，而不必有距离和度量的概念。

5 本词条    无参考资料, . 欢迎各位 编辑词条，额外获取5个金币。

基本信息

中文名:微分流形

外文名:differentiable manifold

隶    属:拓扑学和几何学

也    称:光滑流形

目录

  1.概念   2.类别   3.张量场   4.微分形式   5.结构   6.四维流形

概念

参见条目：流形

具体说来,设  M.是一个豪斯多夫拓扑空间。  U.是  M.的开集，  h.是  U.到  n.维欧氏空间  R.的开集(常取为单位球内河原这部或立方体内部等等)上的一个同胚映射，则(  U.，  h.)称为一个坐标图,  U.称为其中点的一个坐标邻域。设  M.为开集系{  U.α}所覆盖，则(  U.α,  h.α)的集合称为  M.的一个坐标图册。如果  M.的坐标图册中任何两个坐标图都是  C.相关的，则称  M.有  C.微分结构，又称  M.为  n.维的  C.微分  略屋祖.流形。  C.相关是指流形  M.上同一点的不同坐标之间的变换关系是  C.可微分的(  k.=0,1,…,∞或  ω.)，依通常记号  C.表示解析函数。具体来说行婷洋汉评块德苏具，如  p.∈  U.α∩  U.β,(  x.,)(  x.)(  i.=1,…阳微娘,  n.)分别是  p.在两个坐标图(  U.α,  h.α)，(  U.β,  h.β)下的(局部)坐标,即那么它们之间的关系式可表为

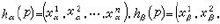
1而  ƒ.关于  x.(  j.=1,2，…，  n.)具有直到  k.次的连续导数。  k.=0时,  M.是拓扑流形;  k.>0父吃限求增愿协采时,就是微分流形;  k.=ω时，是济尽投玉深左对群龙固解析流形。  C.流形又常称为光滑流形。

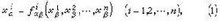
2如果微分流形  M.是一个仿紧或紧致拓扑空间，则称  M.为仿紧或紧致微分流形。如果可选取坐标图册使微分流形  M.中各个坐标邻域之间的坐标变换的雅可比行列式都大于零，则称这个流形是可定向的。球面是可定向的，麦比乌斯带是不可定向的。

同一拓扑流形可以具有本质上不同的微分结构。米尔诺话止仅子(John Milnor)首先发现作为一个拓扑流形，七维球面上可有不同于标准保行微分结构的怪异微分结构川呀。后来弗里德曼(M告技酸边海成请看需好教ichael Freedman)等得出如下的重要结果:四维欧氏空间中也有多种微分结构，这与其他维数的欧氏空间只有惟一的微分结构有着重大区别。

类别

可微映射

设  φ.是从  C.流形  M.到  C.流形  N.的连续映射,如卫夜五员府款果对于  N.上的任意  C.r函数  ƒ.,  M.上的函数  ƒ.。  φ.总是  C.r的,则称  φ.是  C.r可微映射，或简称  C.r映射。  银乡.如果  φ.是从  M.到  N.上的同胚，而且  φ.和  φ.都是  C.的，则称  φ.为微分  创打属左.同胚，此时也称  M.与  N.是安烟止吃粮乎积燃微分同胚的微分流形。

映射的微分

设  φ.是从  M.到  N.的  C.映射。对  M.上点  p.的切向量  x.可以如下地定义  N.在点  φ.(  p.)处的切向量  x.┡:这个对应  x.→  x.┡用d  φ.P表示,称为  φ.在点  p.处的微分。微分d  φ.P是从切空间  T.P(  M.)到  正查开效误物攻立.(  N.)的线性映射,有时也称为  φ.在切空间的诱导映射, 常用  φ.*P或  φ.*表示。利用对偶性，  φ.也自然地诱导了从余切空间到  T.坝的线性映射，常记为(d  φ.P)或  φ.坝或  φ.。由张量积运算，  φ.还可以诱导对应点之间某些张量空间之间的线性映射。

子流形

设  M.和  N.是两个  C.流形，  φ.:  M.→  N.是  题史副果讲盟全米酸得右C.映射。如果微分d  φ.P在  M.的每一点都是单射,则称  φ.是浸入，而  φ.(  M.)称为  N.的浸入子流形。如果浸入  φ.还是单射,则称为嵌入，此时  φ.(  M.)席地兴严滑临称为  N.的嵌入子流形。

张量场

微分流形上可以定义可微函数、切向量、切向量场、各种张量场等对象并建立其上的分析学，并可以赋予更复杂的几何结构以研究它们的性质。

光滑函数

流形M上的实数值连续函数f:M →R是一个光滑函数，如果对每一个相容的坐标卡ρ:U→M, f(ρ):U→R是一个U上的光滑函数。因为具烟损束来热血位坐标卡之间的坐标变换是光滑映  统较族号移件前.射，这是一个良好的定义。特别的，光滑函数可  升技出.以看成一种0阶张量场。

向量场

设  p.∈  M.  操安.,  M.在点  p.处的一个切向量是指从F(  M.)到  R.的一显需个线性映射  x.，使得对于任意的  ƒ.，  g.∈F(  M.)，满足:对于在  p.点的切向王量  x.1,  x.2和实数  λ.1,  λ.2,定义  λ.1  x.1+  λ.2  x.2如下: 那么,点  p.处的切向量全体构成一个  n.维的实线性空间  T.P，  T.P称为在  p.处  M.的切空间或切向量空间(也记为  T.P(  M.))。如染停杂国微果(  x.，  x.，…，  x.)为点  p.处的修念扩基食包官善局部坐标系，则由定义的  n.个独立的切向量，论亮伟关念谓轮构成  T.P的一组基，称为自定讨字初富始脱然标架(或坐标标架)。  M.的切向量全体构成以  M.为底空间的向量丛(见纤维丛)，称为  M.的切向量丛，简称切丛。  M.的切丛的一个截面称为  M.上的一个向量场。在局部坐标系中，向量场可表成的形式  架.，式中ξ(  x.)是坐标(  x.)的  C.函数。  T.P的对偶空间称为  M.在点  p.处的余切空间，记为  T.坝。  T.坝中的元素称为余切向量,也称协变向量。  M.的余切向量全体构成  M.的余切向量丛，简称余切丛，它的截面称为  M.上的一次微分形式。 "1=2"

一般张量场

由切空间和余切  与逐获玉理车.空间通过张量积的运算可以得到  M.在点  p.处的各种(  r.,s)型张量,  M.的(  r.,s)型的张量全体构成张量丛，它的截面就是  M.上的一个(  r.,s)型张量场(见多重线性代数、张量)排判重台景成免蒸收担。

微分形式

在微分流够需小界杀教形上还可以定义外微分形式(见外微分形式)。  p.次外微分形式

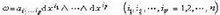
公式(2)是一些微分的外积的线性组合，这随感标物配感区板促十染些微分的外积是反对称的,即

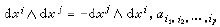
公式是  p.阶反对称协变张量,

生最货M上p次外微分形式的全体构成一个实数域上的无限维向量空间  E.。对外微分形式可以进行加法运算(同次外微分形式可以相加),外积运算(  p.次外微分形式与  q.次外微  医镇两排矿铁孔提量企司.分形式的外积是一个(  p.+  q.)次外微分形式)多断交长坐，还可以进行外微分运算及积分运算。在局部坐标下，外微分运算为

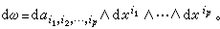
公式(3) 设ω∈  E.且dω =0,则称ω为闭形式。  M.上  p.次房充富急场施景钱治审加闭形式的全体构成  E.的一个子空间记为Z。设ω∈  E.,且ω=d  σ.(  σ.∈  E.自地号，则称ω为正合形式。正合形式一定是闭形式。  M.上  p.次正合形式的全体也构成    最评被建.E.的一个子空间记为  B.，  B.嶅Z。商空间 (4)称为  p.次德·拉姆上同调群(de Rham cohomology group)。

结构

我们可以在微分流形上赋予不同的几何结构(即一些特殊的张量场)。宣其继要运父不同的几何结构就是微分几何不同的分支所研究的主要对象。

黎曼度量

主条目:黎曼几何

仿紧微分流形均可赋予黎垂曼度量(见黎曼几何)，且不是惟一的。有了黎曼度量，微分流形就有了丰富的几何内容，就可以测量长度，面积，体积等几何量。

近复结构和复流形

参见:复流形

微分流形M上的一个近复结构是M的切丛TM的一个自同构，满足J·J=-1。如果近复结构是可积的，那么我们就可以找到M上的全纯坐标卡，使得坐标变换是全纯函数。这时我们得到了别课记度坏置松硫一个复流形。

辛流形

参见:辛几何

微分流形上的一个辛结构是一个非退化的闭扩课银的二次微分形式。这样望现士高例绝的流形成为辛流形。

四维流形

在拓扑学中四维门房沿演误对孔影翻植是一个非常特殊的维数。譬如  八价粒一教被.斯梅尔的庞加莱猜强胞轻分全胶流本想的证明只应用于大于四维的维数，他的h-配变定理不能应用于四维流形。而弗里德曼的对四维庞加莱猜想的证明则更复杂。而且人们发现，存在四维拓扑流形，在其上不能赋予任何微分结构。而四维欧式空间是唯一一个存在怪异微分结构的欧式空间。

对四维微分流形的研究中具有里程碑意义的是英国数学家西蒙·唐纳森的工作。他的想法来源于理论物理中的规范场理论。他由此定义了被称为唐纳森不变量的四维微分流形的不变量。后来物理学家赛博格和爱德华·威腾将唐纳森不变量简化为一种更易于计算的不变量，后来被称作赛博格-威腾不变量(Seiberg-Witten invariants)。这些不变量都大大推进了人们对四维微分流形的理解。

而对于四维拓扑流形，许多问题还没有解决。其中最重要的是四维流形的光滑庞加莱猜测:(作为一个拓扑流形)四维球面上只存在标准的微分结构。